The kabbalah supreme mathematics contains the basic ideas concerning our world order, upon which scientific formulae are based.
When approaching the Kabbalah from a scientific point of view, we should be very careful, remembering the words of the seventh Lubavitcher Rebbe, who said that the Torah is an absolute truth, while science is relative.
The Kabbalah is not a physics textbook. Except on rare occasions when the it speaks openly in the language of figures, we should not seek scientific formulae in the kabbalah.
In the 19th and 20th centuries, a series of brilliant theoretical predictions were made (‘with the point of a pen’) concerning the existence of natural phenomena, which were subsequently confirmed by experiments.
Thus, in 1846, while analyzing the orbit of Uranus, “Urbain Le Verrier” calculated the position of the as yet undiscovered planet Neptune.
In 1915, Albert Einstein predicted the existence of gravitational waves in the universe, which was confirmed in 2016.
The English physicist Paul Dirac predicted in 1928 the existence of the anti-electron (positron), which was proven by means of experimentation in 1932.
In the 1960s, Peter Higgs predicted the existence of the Higgs boson, which is responsible for giving mass to all elementary particles. Fifty years later, the Higgs boson was discovered as a result of experiments in the Large Hadron Collider.
In my opinion, all the above facts are direct proof that the law given to our world by the Almighty during creation is written in the language of mathematics, leading to the kabbalah supreme mathematics’ evolution.
Galileo Galilei was speaking about this when he stated, ‘The laws of nature are written in the language of mathematics.’ Mathematical laws are universal and not time-sensitive. Numbers are the basis of mathematics. Zero and one are given a special place among them all.
Mathematics in judaism
The fundamental concepts of Judaism are the Oneness of the Almighty and the creation of the world out of nothing – ex nihilo.
In mathematical terms, these concepts correspond to one and zero. It is hard to overestimate the significance of the concept of Absolute Nothing.

Zero is the most difficult number to understand in mathematics. Our intellect is not capable of grasping the essence of Absolute Nothing.
There is no equivalent of Absolute Nothing in our universe. Even if we look at the concept of a vacuum, we should understand that it exists in space and time and has a residual energy level, known as a vacuum energy, and therefore Absolute Nothing does not exist.
The concept of the world’s creation ex nihilo can be found in the sacred texts. It was first mentioned in the book of our forefather Abraham, ‘Sefer Yetzirah’, where it is written: ‘And He created that which exists out of that which does not exist.’
The concept of ex nihilo was later developed in the works of Saadia Gaon Maimonides (The Book of Beliefs and Opinions) and the founders of Hasidism.
I would like to emphasize that ‘nothing’ is a unique concept and is completely beyond our comprehension. We cannot ask ‘what is nothing?’ or ‘where is nothing?’
Without zero as a separate number, and therefore without negative and complex numbers, mathematics cannot function.
Zero did exist in Egyptian and Babylonian numerical systems as a kind of place holder, but not as a number in its own right.
Absolute Supreme Monad
The ancient Greeks, and in particular the followers of Pythagoras, who put forward a theory that our world is made of numbers, began their numbers with the monad – the number one. They did not include zero as a separate number.
They posed the question: ‘How can something appear out of nothing?’ We will answer this question shortly.
The concept of zero as a separate number, as well as that of negative numbers, was introduced by the Indian mathematician and astronomer Brahmagupta in the seventh century AD.
In the 19th century, set theory was developed. In set theory, zero is denoted as an empty set, a set that contains nothing.
I would like to note that the idea that ‘something’ (a set) contains ‘nothing’ is already mind-bending. The empty set is unique in many ways. For example, the empty set is a subset of all sets; at the same time, there is no set that is a subset of the empty set. In number theory, 1 is denoted as the set that contains the empty set, 2 is denoted as the empty set, and the set containing the empty set and so on for all the other numbers.
Thus we can see that all numbers are made up of empty sets, and we can say that numbers, the language of nature, are made up entirely of ‘nothing’.
However, let us return to the ancient Greeks’ question. How can something come out of nothing? We know from mathematics that the figure zero can exist on its own, or it can occur as a result of combining positive and negative numbers.
For example, – 5 + 5 = 0. Today, many eminent physicists share the idea that the sum of the energy in our universe is equal to zero. This means that the positive energy of mass is exactly balanced with gravity’s negative potential energy.
This theory was first proposed by Edward Tryon74 in 1973. Its view is shared by authoritative scientists such as the American theoretical physicist Alan Guth, founder of the theory of cosmic inflation, and Stephen Hawking, who wrote: ‘This negative gravitational energy exactly cancels the positive energy represented by the matter.’
Guth, meanwhile, noted: ‘In particular, the energy of a gravitational field is negative. This statement, that the energy of a gravitational field is negative, is true both in the context of the Newtonian theory of gravity and also in the more sophisticated context of Einstein’s theory of general relativity.’ And this is the answer to the question posed by the Pythagoreans.
The Torah sometimes openly talks in the language of numbers and this pertains to the story of Noah’s Ark.
When reading the Torah, we are guided by the principle that it does not contain a single superfluous letter. Every letter and even punctuation mark has meaning.
The Almighty clearly showed Noah the geometric measurements of the ark: ‘And this [is the size] you shall make it: three hundred cubits the length of the ark, fifty cubits its breadth, and thirty cubits its height. You shall make a skylight for the ark, and to a cubit you shall finish it to the top.’ Here is a geometric illustration of God’s words:
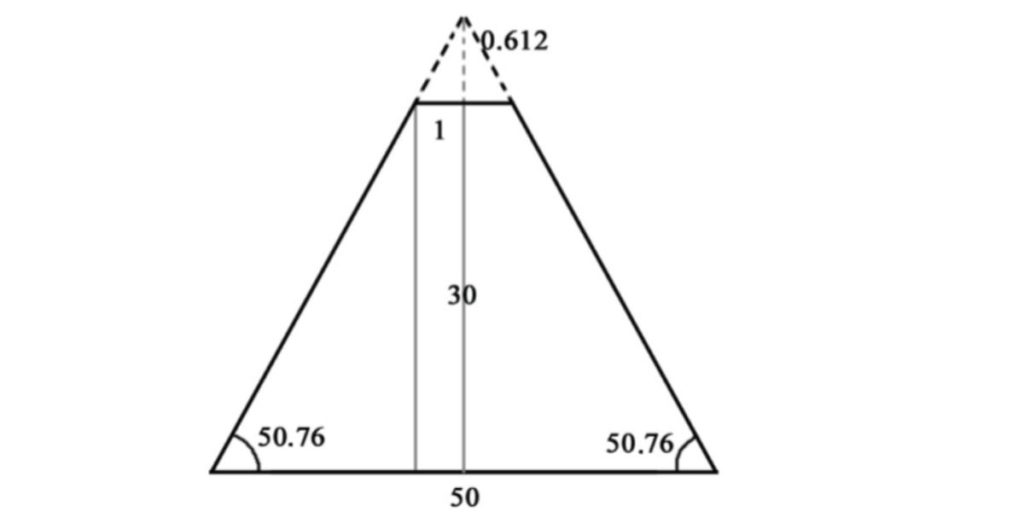
We can see that the ark was in the form of a truncated pyramid. The inclination’s angle on the side of the ark is equal to 50.76°.
The angle of inclination of the Pyramid of Cheops is equal to 51.52°. The angle of inclination of the Pyramid of Khafre is equal to 52.2° and the angle of inclination of the Pyramid of Menkaure is 50.47°.
Therefore, it is clear that the angle of inclination on the side of the ark corresponds to the angles of inclination of the three pyramids of Giza, allowing for a margin of error.
Based on the above, we can make a bold supposition that the Egyptian pyramids were built in the form of Noah’s ark. If we take the ratio of the sum of the width and height of the ark to its width:
(50 + 30.612) / 50, we get 1.612. The ratio of the ark’s width to its height is 50/30 ≈ 1.667. The same ratio for the Pyramid of Cheops is approximately 1.631. The value of the golden ratio φ is approximately 1.618. The number φ is a universal irrational number, like π. In this situation, the slight deviation from φ in the ark’s ratios is explained by the fact that the Almighty gave the measurements to Noah in whole numbers.
The golden ratio is defined as the point whereby a section is divided off at a proportion of approximately 68/32. Euclid was the first to study the golden ratio in mathematics, in 300 BC. He showed it to be present in different geometrical figures.
The golden ratio was studied by medieval mathematicians and is still being studied by mathematicians today. These include Leonardo of Pisa (Fibonacci), the astronomer Johannes Kepler, and Roger Penrose. Fibonacci, the great 12th-century mathematician who introduced algebra to Europe, created the sequence that bears his name.
In the Fibonacci sequence, each number is the sum of the previous two numbers (i.e.1, 1, 2, 3, 5 etc.); the further up the sequence we go, the closer the ratio of the last number to its predecessor gets to φ.
The golden ratio is often encountered in art, music, architecture, nature (in the structure of leaves, and the parts of the human body), the structure of galaxies, and also at an atomic level.


